Próbalap MCBJ
Már az ókori görögök is azt feltételezték, hogy az anyag atomokból épül fel. Ezt a hipotézist a 20. század elején számos kísérlettel sikerült bizonyítani, azonban ahhoz, hogy képet tudjunk készíteni egy anyag felületén lévő atomokról egészen 1981-ig kellett várni, amikor Gerd Binnig és Heinrich Rohrer megépítették az első pásztázó alagútmikroszkópot, amiért öt évvel később Nobel-díjjal jutalmazták őket.
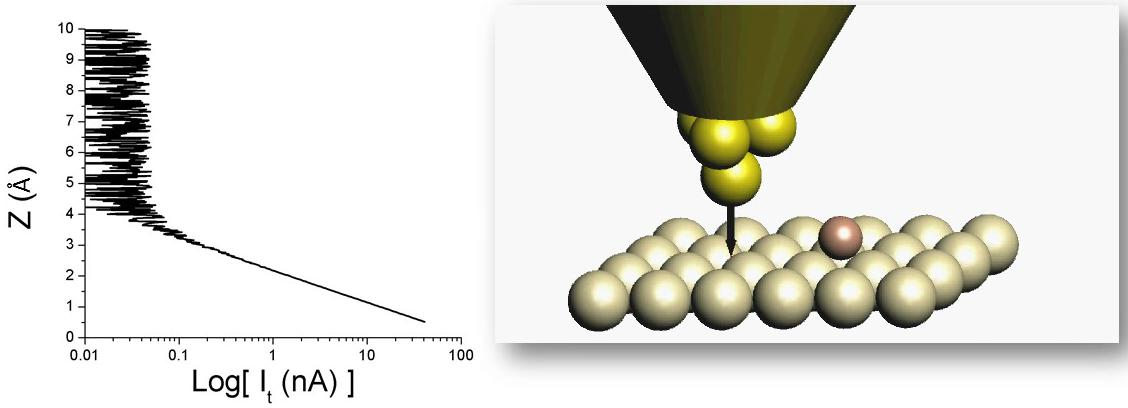
Az alagútmikroszkóp működése az elektronok hullámtermészetének egy speciális következményén alapul, miszerint két egymáshoz közel vitt fémdarab között akkor is folyik áram, ha azok nem érnek össze. Ezt az áramot kvantummechanikai alagútáramnak hívják, melynek érdekes tulajdonsága, hogy a két fém távolságától nagyon érzékenyen függ: ha csak egy fél atom-atom távolsággal csökkentjük a rés szélességét, akkor az áram tízszeresére nő. Ezt a viselkedést demonstrálja az 1. ábra.
1. ábra. Egy hegyes fémtű és egy fémfelület közé feszültséget kapcsolunk, és miközben a tűt közelítjük a felülethez, mérjük az áramot. Amíg távol van a tű a felülettől, az áram olyan kicsi, hogy az árammérőnkkel nem tudjuk felbontani. Ahogy a tű és a felület távolsága összemérhetővé válik két szomszédos atom távolságával véges áramot kezdünk el detektálni. Az áramot ún. logaritmikus skálán ábrázoltuk, azaz egy osztás az áram tízszeres megváltozásának felel meg. A tű és a felület távolságát Angström mértékegységben adtuk meg, ami 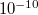 méternek felel meg. Forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. méternek felel meg. Forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.
|
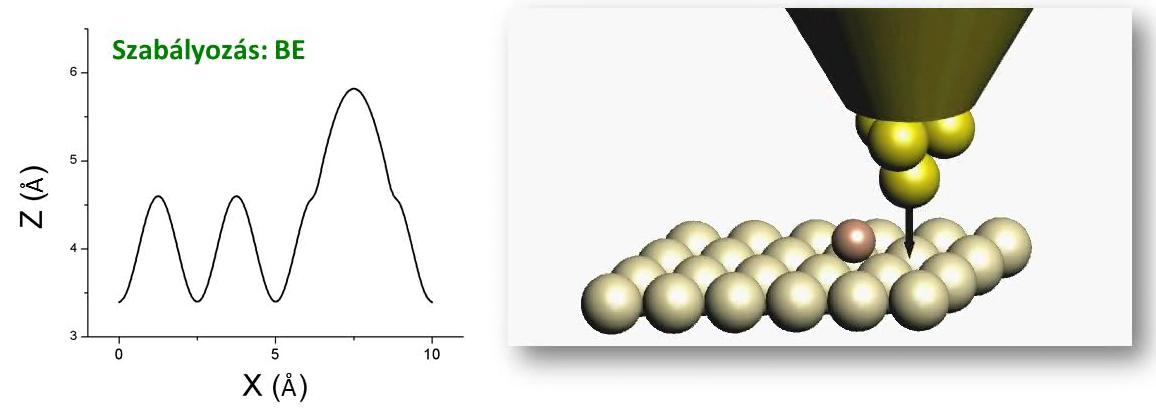
Egy nem túl hegyes tű (pl. egy ollóval elvágott fémszál) esetén is találunk a tű hegyén egy atomot, ami egy kicsit közelebb van a felülethez a többi atomnál. Az érzékeny távolságfüggés miatt az alagútáram jelentős része ezen egyetlen atomon keresztül fog folyni. Ezt kihasználva a fémfelületet akár atomi felbontással is feltérképezhetjük a tű megfelelő mozgatásával. A fémfelülettel párhuzamosan pásztázunk a tűvel, miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest (2. ábra). A tű mozgását számítógéppel rögzítve rekonstruálhatjuk a felület képét.
| 2. ábra. Miközben a tűt a felülettel párhozamosan konstans sebességgel mozgatjuk, a felületre merőleges irányban úgy pozicionáljuk, hogy az alagútáram, azaz a minta és a tű távolsága konstans maradjun (bal oldal). A tű mozgása alapján rekonstruálhatjuk a felület képét akár atomi felbontással (jobb oldal). Forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
Az alábbi ábra egy grafit felület pásztázó alagútmikroszkóppal készített, atomi felbontású képét mutatja be.
| 3. ábra. Atomi felbontású kép grafit minta felületéről, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. |
A pásztázó alagútmikroszkóp tűjét piezoelektromos kerámiák segítségével mozgathatjuk akár atomi precizitással. Piezo kerámiával a hétköznapokban is találkozunk, például az öngyújtó egy piezo hasáb hirtelen megnyomásával hoz létre nagy feszültséget, és az így keletkező szikra gyújtja be a lángot. Piezo mozgatónál pont fordítva járunk el, a piezo hasábra elektromos feszültséget kapcsolunk, és ennek hatására a hasáb egy kicsit megnyúlik.
A pásztázó alagútmikroszkóp nem csak képalkotásra, hanem a minta felületének atomi felbontású manipulációjára is alkalmas: a tű segítségével atomokat lehet mozgatni a felületen. Ezzel a technikával hozták létre a 4. ábrán látható kör alakzatot, amit 48 vas atom alkot egy réz felületen. Az alagútmikroszkópos felvételen jól megfigyelhetőek a kör belsejében kialakuló elektron-állóhullámok.
| 4. ábra. Elektron-állóhullámok egy atomokból kirakott kör belsejében. Forrás: Wikipedia |
Egy pásztázó alagútmikroszkópot arra is használhatunk, hogy létrehozzuk az elképzelhető legvékonyabb nanovezetéket. Ha a mikroszkóp tűjét a felületbe nyomjuk, majd elkezdjük visszahúzni, akkor egy nanovezetéket tudunk húzni a felület és a tű között. A széthúzás közben a nanovezeték egyre vékonyodik, majd a szétszakadás előtt már csak egyetlen atom köti össze a két oldalt.
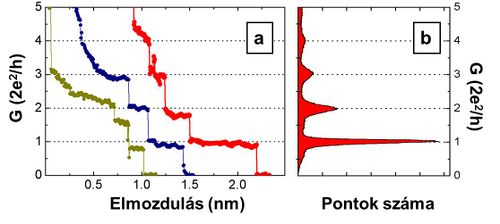
Ha egy pár atom átmérőjű nanovezeték szakítása közben mérjük a vezetőképességet (az ellenállás reciprokát, 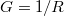 ), akkor a 5. ábra bal oldalán látható vezetőképesség görbéket kapjuk: a tű emelése közben a vezetőképesség nem folytonosan, hanem lépcsőzetesen csökken. Amikor egy lapos platót látunk, akkor a vezeték geometriája nem nagyon változik, csak rugalmasan távolodnak egymástól az atomok. Az ugrásnál viszont hirtelen átrendeződnek az atomok, és az ugrás után már kevesebb atom köti össze a két oldalt. A szétszakadás előtti utolsó lépcsőnél az áram már csak egyetlen atomon keresztül folyik.
), akkor a 5. ábra bal oldalán látható vezetőképesség görbéket kapjuk: a tű emelése közben a vezetőképesség nem folytonosan, hanem lépcsőzetesen csökken. Amikor egy lapos platót látunk, akkor a vezeték geometriája nem nagyon változik, csak rugalmasan távolodnak egymástól az atomok. Az ugrásnál viszont hirtelen átrendeződnek az atomok, és az ugrás után már kevesebb atom köti össze a két oldalt. A szétszakadás előtti utolsó lépcsőnél az áram már csak egyetlen atomon keresztül folyik.
| 5. ábra. Atomi méretű arany nanovezetékek szakítás közben felvett vezetőképesség-görbéi (jobb oldal). Az egymás tutáni szakítások jellegre hasonló, de a részletekben különböző vezetőképsség-görbéket adnak. Sok szakítás vezetőképesség-görbéi alapján felrajzolhatunk egy vezetőképesség-hisztogramot (bal oldal), melyben a csúcsok a gyakran kialakuló atomi konfigurációk vezetőképességeit adják meg. |
Egyetlen arany atomon keresztül a vezetőképesség közel van egy univerzális állandóhoz, az úgynevezett vezetőképesség kvantumhoz, melyet az elektron töltése, és Planck-állandó definiál: 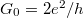 . Ez a vezetőképesség körülbelül
. Ez a vezetőképesség körülbelül 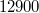 Ohm ellenállásnak felel meg.
Ohm ellenállásnak felel meg.
Ha a szakítás után a két elektródát összenyomjuk, a szakítási felületen az atomok újra összekapcsolódnak, így a nanovezeték szakítását újra és újra megismételhetjük. Több ezer szakítás során felvett vezetőképesség-görbéből hisztogramot készíthetünk, melyben csúcsok jelennek meg a gyakran előforduló atomi elrendeződések vezetőképesség-értékeinél. Az első csúcs az egyatomos kontaktus vezetőképességénél, azaz a vezetőképesség kvantumnál jelenik meg (5. ábra, jobb oldal).
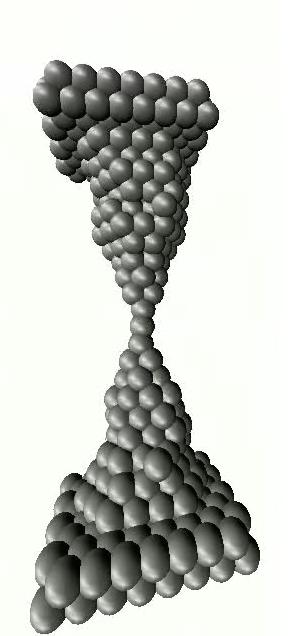
Arany nanovezetékeknél egy további érdekes jelenséggel is találkozunk. A szétszakadás előtti utolsó vezetőképesség-plató hosszát megmérve gyakran lényegesen nagyobb hosszt kapunk, mint amit egy atom méretéből várnánk. Megmutatható, hogy egy egyatomos arany kontaktus további széthúzása során az nem mindig szakad szét, hanem akár hét atomból álló atomi aranyláncot is húzhatunk (6. ábra).
| 6. ábra. Atomlánc húzása a nanovezeték szakítása közben (számítógépes szimuláció). |
Hétköznapi körülmények között egy 7 méter hosszú vezeték ellenállása pontosan hétszerese egy egyméteres vezetékdarabénak. Atomi méretskálán viszont teljesen más viselkedést tapasztalunk. Egy hétatomos aranylánc ellenállása pontosan megegyezik a háromatomos láncéval, vagy az egyatomos kontaktuséval, hiszen ha az elektronok egyszer bejutnak a láncba, akkor már a lánc hosszától függetlenül ütközés nélkül átjutnak a túloldalra.
Atomi méretű nanovezetékek segítségével a jelenlegi félvezető tranzisztoroknál lényegesen kisebb elektronikai építőelemek hozhatók létre, például a Fizika Tanszék laboratóriumában egy olyan rendszert tanulmányozunk, amiben pozitív feszültség hatására kialakul egy nanovezeték a két elektróda között, negatív feszültséggel viszont megszakíthatjuk ezt a vezetéket. Ez gyakorlatilag egy memóriaelem, amivel pár nanométeres skálán tárolhatunk információt. Ezen kívül az atomi méretű kontaktusokat arra is használhatjuk, hogy egyedi molekulák elektromos vezetési tulajdonságait tanulmányozzuk. Miután szétszakad a kontaktus, egy olyan keskeny nano-rés jön létre, amihez a megfelelő kémiai csoportokkal rendelkező parányi molekulák szeretnek kötődni. Így a két elektróda között akár egy egyetlen molekulából álló hidat hozhatunk létre. Egyedi molekulákból készített nanoáramkörök vizsgálatával a nanofizikán belül egy egész tudományterület, az úgynevezett molekuláris elektronika foglalkozik. A kutatások fő célja, hogy a jelenleg több százezer atomból álló tranzisztorokat egyedi molekulákból felépülő elektronikai eszközök váltsák fel. Laboratóriumi körülmények között már sikerült létrehozni olyan tranzisztort, aminek az aktív tartománya egyetlen fullerén molekulából áll, és az erősítést egyetlen elektron végzi.
Mérési feladatok
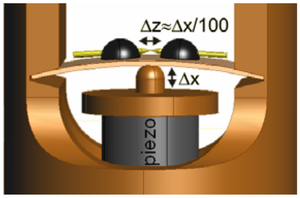
A foglalkozás keretében először megismerkedhettek egy saját fejlesztésű pásztózó alagútmikroszkóppal. Ezután mérőpárokba rendeződve önállóan kísérletezhettek egy olyan esztközzel, mely kialakításában sok hasonlóságot mutat egy pásztázó alagútmikroszkóppal. Az ún. törőkontaktus elrendezés elvét a 7. ábra szemlélteti. Egy fémszálat ragasztóval, vagy forrasztással két közeli ponton egy rugalmas lapkához rögzítünk. A két rögzítési pont között egy penge segítségével elvékonyítjuk a fémszálat. A rugalmas lapkát a két végénél megtámasztjuk, középen pedig egy léptetőmotorral forgatott tengely, illetve egy piezomozgató segítségével elkezdjük hajlítani. A lapka hajlítása közben a fémszál elszakad. Ezzel az elrendezéssel nem lehet a nanovezeték tengelyére merőleges irányban pásztázni, de vizsgálhatjuk a kvantummechanikai alagútáramot, megmérhetjük egy egyetlen atom átmérőjű nanovezeték ellenállását, és kipróbálhatjuk az alagútmikroszkópnál használt szabályozástechnikát. Az elrendezés előnye az alagútmikroszkóphoz képest a kiemelkedő mechanikai stabilitás. Kiszámolható, hogy a piezomozgató 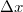 elmozdulása nagyságrendileg
elmozdulása nagyságrendileg 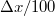 elmozdulást eredményez a vezeték két oldal között, így minden mechanikai rezgés, vagy hőtágulásból adódó elmozdulás egy százas faktorral csökkentett mértékben jelenik meg a nanovezeték megnyúlásában. Ennek köszönhető, hogy egy viszonylag egyszerű berendezéssel végezhetünk olyan kísérleteket, melyekben atomi méretskálájú nanoszerkezetek tulajdonságait vizsgálhatjuk.
elmozdulást eredményez a vezeték két oldal között, így minden mechanikai rezgés, vagy hőtágulásból adódó elmozdulás egy százas faktorral csökkentett mértékben jelenik meg a nanovezeték megnyúlásában. Ennek köszönhető, hogy egy viszonylag egyszerű berendezéssel végezhetünk olyan kísérleteket, melyekben atomi méretskálájú nanoszerkezetek tulajdonságait vizsgálhatjuk.
| 7. ábra. Törőkontaktus elrendezés vázlata |
A mérési elrendezés összeállítása
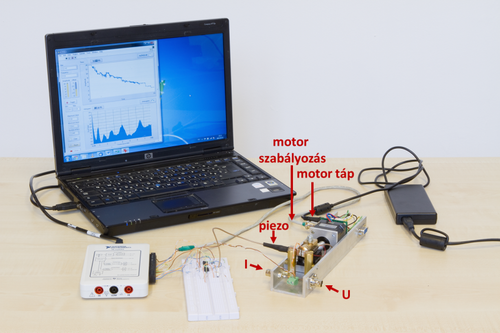
A méréshez használt elrendezést a 8. ábra szemlélteti. Egy alumínium konzolba rögzítve található a léptetőmotor, a piezomozgató és a rugalmas lapkára rögzített fémszál. A motorhoz egy tápegység tartozik. A motor és a piezomozgató vezérlését, illetve a vezetőképesség mérését egy National Instruments MyDAQ típusú, számítógéphez csatlakoztatott adatgyűjtő kártyával végezzük. A méréshez szükséges kiegészítő áramköröket egy próbapanelen állíthatjuk össze.
| 8. ábra. A méréshez használt eszközök |
A laprugóra rögzített fémszálat a 9. ábrán láthatjuk kinagyítva.
| 9. ábra. Nyáklapból készült rugalmas lapkára forrasztott fémszál |
A TRINAMIC - PD3-013-42 léptetőmotor az alumínium konzolra rögzített négypólusú mikrofoncsatlakozón keresztül vezérelhető. A négy pólusból háromra digitális jeleket küldünk a mérőkártyáról. Az egyik pólussal a motor ki és bekapcsolható (ENABLED), a másik pólussal a motor forgásiránya állítható (DIRECTION), a harmadik pólusra pedig egy rövid pulzust küldve a motor egy lépést tesz, azaz körülbelül 0.1 fokkal fordul el. A negyedik pólusra a digitális jelek földje (DGND) kerül. A mellékelt kábellel csatlakoztathatjuk a motort a mérőkártyához. A kábel színkiosztása: ENABLED - Kék, DIRECTION - Zöld, STEP - Narancs, DGND - Barna.
A mérőkártya csatlakozóinak kiosztását a 10. ábra mutatja.
| 10. ábra. National Instruments MyDAQ mérőkártya csatlakozói |
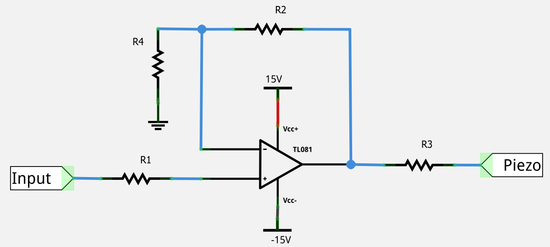
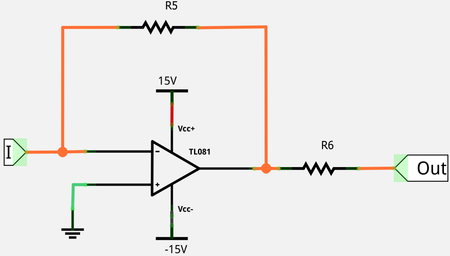
A finom mozgatáshoz Piezomechanik PSt150/3.5x3.5/20 típusú piezomozgatót használunk, mely -30 - +150 V tartományban működtethető, a teljes feszültségtartomány 28 μm elmozdulásnak felel meg. A piezot nem vezérelhetjük közvetlenül a mérőkártyáról, hiszen az nem tudna elég nagy áramot kiadni, így egy erősítőt kell közbeiktatnunk. Az erősítőáramkört a 11. ábra kapcsolása alapján magatoknak állítjátok össze a próbapanelen.
| 11. ábra. A piezomozgatóhoz használt erősítő kapcsolási rajza |
Az áramkör működését az ideális műveleti erősítő modellje alapján könnyen megérthetjük. A háromszög jelű műveleti erősítőt úgy modellezhetjük, hogy a "+" és "-" jelű bemenetek közötti feszültség elhanyagolható, és mindkét bemenet óriási bemeneti ellenállással rendelkeznek, azaz ezeken a bemeneteken gyakorlatilag nem folyik áram. Ennek köszönhetően a "+" bemenet felveszi a bemeneti feszültségét, 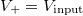 . A fenti modell alapján a "-" bemenet is a
. A fenti modell alapján a "-" bemenet is a 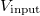 feszültséget veszi fel. Az erősítő kimenete ennek megfelelően
feszültséget veszi fel. Az erősítő kimenete ennek megfelelően 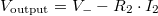 feszültséget vesz fel, ahol
feszültséget vesz fel, ahol 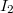 az
az 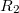 ellenálláson folyó áram. Mivel a "-" bemeneten nem folyik áram, ezért
ellenálláson folyó áram. Mivel a "-" bemeneten nem folyik áram, ezért 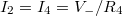 is felírható. A fentieket összesítve
is felírható. A fentieket összesítve
![\[V_\mathrm{output}=V_\mathrm{input}\left(1-\frac{R_2}{R_4}\right)\]](/images/math/4/9/f/49f24310001d0e636bf3899463bb2732.png)
egyenlettel írható fel az erősítés a 11. ábrán alkalmazott kapcsolás esetén.
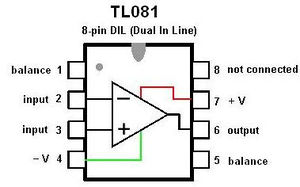
Műveleti erősítőként a TL081 típusú IC-t használjuk, melynek lábkiosztása a 12. ábrán látható.
| 12. ábra. TL081 műveleti erősítő lábkiosztása |
Az erősítőt a MyDAQ kártya +15V illetve -15V kimeneteiről tápláljuk. Az erősítő 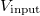 bemeneti feszültségét a kártya AO1 analóg kimeneti csatornájáról vezéreljük. Ellenállásként
bemeneti feszültségét a kártya AO1 analóg kimeneti csatornájáról vezéreljük. Ellenállásként  Ohm,
Ohm, 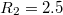 kOhm,
kOhm,  Ohm,
Ohm, 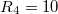 kOhm értékeket alkalmazzunk, mellyel 1.25-szörös erősítést valósítunk meg. A piezomozgató BNC csatlakozójának belső pontjára az erősítő kimenetét, külső pontjára pedig az analóg földet (AGND) csatlakoztassuk.
kOhm értékeket alkalmazzunk, mellyel 1.25-szörös erősítést valósítunk meg. A piezomozgató BNC csatlakozójának belső pontjára az erősítő kimenetét, külső pontjára pedig az analóg földet (AGND) csatlakoztassuk.
A fémszál U jelű csatlakozóját (lásd 8. ábra) kössük a kártya AO0 kimenetére, a BNC külső pontját megintcsak földeljük le (AGND). Az I jelű csatlakozón keresztül kell áramot mérnünk, amihez szintén saját erősítőt állítotok össze a 13. ábra kapcsolása alapján. A fenti meggondolások alapján az erősítő kimeneti feszültsége 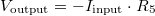 . (Ezt hívjuk áramerősítő kapcsolásnak.) Az
. (Ezt hívjuk áramerősítő kapcsolásnak.) Az 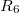 ellenállás legyen
ellenállás legyen 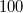 Ohm,
Ohm, 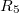 -nek pedig kiindulásként
-nek pedig kiindulásként 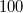 kOhm-os ellenállást válasszunk. Az I jelű csatlakozó külső pontját szintén a földhöz (AGND) csatlakoztassuk.
kOhm-os ellenállást válasszunk. Az I jelű csatlakozó külső pontját szintén a földhöz (AGND) csatlakoztassuk.
| 13. ábra. Áramerősítő áramkör kapcsolási rajza |
Vezetőképesség-hisztogram mérése
Indítsuk el a mérőprogramot (lásd függelék). A mintára adjunk -100mV feszültséget (így kapunk az áramerősítő kimenetén pozitív feszültséget). Először állítsuk a piezot meghajtó háromszögjel amplitudóját maximálísra (a 10V amplitudó +10V és -10V közötti háromszögjelnek felel meg), a nullpontot (OFFSET) pedig állítsuk 0V-ra. Adjuk meg az áramerősítés értékét (100 kOhm-os visszacsatoló ellenállást alkalmazva ez 100000, azaz 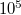 A áramra kapunk 1V kimenőfeszültséget az erősítőn). Először a triggert kapcsoljuk ki, és a motor mozgatásával szakítsuk el a vezetéket. Mikor elszakad a vezeték, a program felső ábráján a mért maximális vezetőképesség (amit az erősítő telítése határoz meg) 0-ra ugrik. Ha jól állítjuk be a motor pozícióját, akkor a piezora adott háromszögjel ismételten elszakítja és összenyomja a vezetéket.
A áramra kapunk 1V kimenőfeszültséget az erősítőn). Először a triggert kapcsoljuk ki, és a motor mozgatásával szakítsuk el a vezetéket. Mikor elszakad a vezeték, a program felső ábráján a mért maximális vezetőképesség (amit az erősítő telítése határoz meg) 0-ra ugrik. Ha jól állítjuk be a motor pozícióját, akkor a piezora adott háromszögjel ismételten elszakítja és összenyomja a vezetéket.
Kapcsoljuk be a triggert, így a felső ábrán csak egy adott vezetőképsségű pont megfelelő szélességű környezetét látjuk. Így kinagyíthatjuk a vezetőképesség-görbék azon szakaszát, ahol már csak pár atom köti össze a két oldalt.
A mérés felbontását javíthatjuk, ha csökkentjük a piezot meghajtó jel amplitudóját. A kártya kimenete a háromszögjel teljes periódusát mindig 100000 diszkrét pontban valósítja meg, így a piezora kiadott szomszédos feszültségpontok annál közelebb vannak egymáshoz, minél kisebb a jel amplitudója. Az amplitudó csökkentésekor az OFFSET állításával találhatjuk meg azt a piezofeszültség-tartományt, melyben el tudjuk szakítani, majd össze tudjuk nyomni a nanovezetéket. Fontos, hogy az alkalmazott amplitudót minden mérésnél jegyezzük fel, hiszen erre szükség van a későbbi számolásokhoz.
Vegyünk fel egy vezetőképeség-hisztogramot, melyen szépen látszik az egyatomos kontaktusnak megfelelő csúcs. Rögzítsünk egyedi görbéket is, melyeken jól látszik a vezetőképesség lépcsőzetes csökkenése. Keressünk olyan görbéket, melyen az utolsó, vezetőképesség-kvantumnál jelentkező plató aránytalanul hosszú a többi platóhoz képest, ezek valószínűleg atomi láncképződésnek felelnek meg.
Alagútáram vizsgálata
Állítsuk a vezetőképeség-görbék ábrájának Y tengelyét logaritmikus beosztásra. Vizsgáljuk a szétszakadt kontaktus alagútáramának változását a piezofeszültség függvényében, ami a logaritmikus skálán közel egyenes kell hogy legyen (lásd 1. ábra). Ehhez az áramerősítést növeljük meg egy nagságrenddel, azaz az 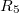 ellenáálást cseréljük le 1MOhm-os ellenállásra. Az alagútáramot nem a szétszakadás után, hanem az összenyomás előtti tartományban érdemes vizsgálni, hiszen a szétszakadás előtt megnyúlik a kontaktus, így miután elszakad távolra ugrik a két elektróda, így azonnal nagyon kicsivé válik az alagútáram.
ellenáálást cseréljük le 1MOhm-os ellenállásra. Az alagútáramot nem a szétszakadás után, hanem az összenyomás előtti tartományban érdemes vizsgálni, hiszen a szétszakadás előtt megnyúlik a kontaktus, így miután elszakad távolra ugrik a két elektróda, így azonnal nagyon kicsivé válik az alagútáram.
Ennél a mérésnél is érdemes a piezomeghajtás amplitudóját lecsökkenteni (1V-os nagyságrendűre), és a triggert használni.
Az alagútáram tízszeres megváltozása hozzávetőlegesen 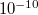 m elmozdulásnak felel meg. Az alagútáram piezofeszültség-függéséből kalibráljátok a mérőszközt, azaz mondjátok meg, hogy 1V piezofeszültség-változás a nanovezeték két oldala között mekkora elmozdulásnak felel meg. Ez alapján pontosítsátok a 7. ábrán szemléltetett leosztási tényezőt, azaz becsüljétek meg, hogy a piezomozgató elmozdulása mennyire csökkentett mértékben jelenik meg a fémszál megnyújtásában.
m elmozdulásnak felel meg. Az alagútáram piezofeszültség-függéséből kalibráljátok a mérőszközt, azaz mondjátok meg, hogy 1V piezofeszültség-változás a nanovezeték két oldala között mekkora elmozdulásnak felel meg. Ez alapján pontosítsátok a 7. ábrán szemléltetett leosztási tényezőt, azaz becsüljétek meg, hogy a piezomozgató elmozdulása mennyire csökkentett mértékben jelenik meg a fémszál megnyújtásában.
Stabilitás mérése
A pásztázó alagútmikroszkóp működése közben a szabályozó áramkör úgy mozgatja a piezot a mintára merőleges irányban, hogy az alagútáram mindig a kívánt célérték (SETPOINT) maradjon. Ha az alagútáram eltér a célértéktől akkor a szabályozó áramkör olyan irányban mozgatja piezot, hogy az aktuális alagútáram és a célérték közti különbség, az ún. hibajel csökkenjen. A szabályozást két paraméterrel lehet jellemezni, az egyik az ún. 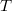 időállandó, ami azt a tipikus időskálát jellemzi, amin belül a szabályozókör válaszolni tud az alagútáram megváltozására. A másik paraméter pedig a
időállandó, ami azt a tipikus időskálát jellemzi, amin belül a szabályozókör válaszolni tud az alagútáram megváltozására. A másik paraméter pedig a 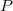 proporcionális tag, mely azt adja meg, hogy egy adott nagyságú hibajel mekkora piezofeszültség-változást eredményezzen.
proporcionális tag, mely azt adja meg, hogy egy adott nagyságú hibajel mekkora piezofeszültség-változást eredményezzen.
Szimuláljuk a mérőberendezésünkön az alagútmikroszkóp szabályozó-mechanizmusát. A szoftverből megvalósított szabályozás nem túl gyors, így időállandónak 10ms-nál kisebb értéket nem választhatunk. 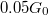 vezetőképesség-célértéket beállítva hangoljuk a szabályozás paramétereit, és próbáljunk olyan beállítást találni, melynél az alagútáram minél kevésbé tér el a célértéktől. Ha ezt sikerült megvalósítani, akkor vizsgáljuk a szabályozó jelet, azaz figyeljük, hogy hogyan kell a piezofeszültséget időben változtani ahhoz, hogy az alagútáram konstans maradjon. A korábbi kalibráció alapján mondjuk meg, hogy egy perces időskálán mennyit mozdulna el a kontaktus szabályozás nélkül. Vizsgáljuk azt is, hogy hogyan reagál a rendszer külső behatásokra, pl. asztal kopogtatása, hanghatás, stb.
vezetőképesség-célértéket beállítva hangoljuk a szabályozás paramétereit, és próbáljunk olyan beállítást találni, melynél az alagútáram minél kevésbé tér el a célértéktől. Ha ezt sikerült megvalósítani, akkor vizsgáljuk a szabályozó jelet, azaz figyeljük, hogy hogyan kell a piezofeszültséget időben változtani ahhoz, hogy az alagútáram konstans maradjon. A korábbi kalibráció alapján mondjuk meg, hogy egy perces időskálán mennyit mozdulna el a kontaktus szabályozás nélkül. Vizsgáljuk azt is, hogy hogyan reagál a rendszer külső behatásokra, pl. asztal kopogtatása, hanghatás, stb.
Függelék
A mérőprogram funkciói
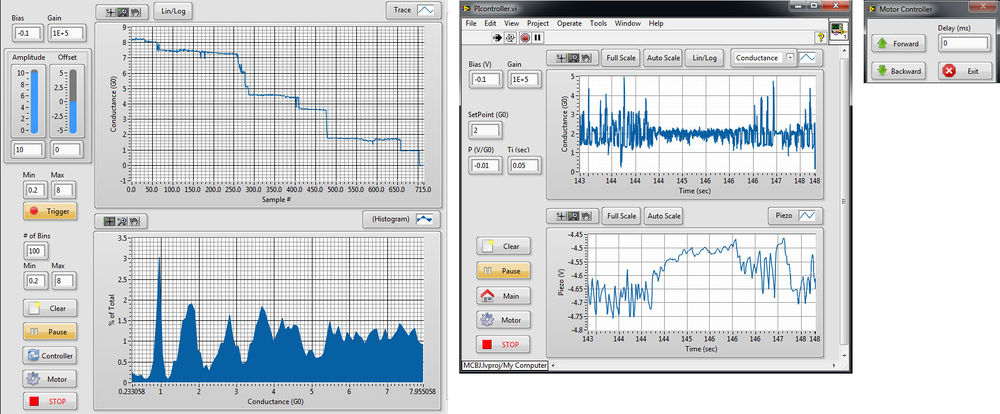
A 12. ábrán látható a mérésvezérlő program különböző funkciókat ellátó ablakai.
| 12. ábra. Mérésvezérlő szoftver. |
Bal oldalon a fő ablak látható, ezt használhatuk a szakítási görbék felvételéhez. A program indulásakor meg kell adni egy fájlnevet, ahova aprogram az adatokat elmenti. A mérés kezdetén állítsuk be a mintára adott feszültséget valamint az áramerősítés mértékét. A piezomozgatót vezérlő háromszögjel paramétereit az 'Amplitude' valamint az 'Offset' feliratú csúszkákkal állíthatjuk. A mért vezetőképesség-értékeket a felső kijelzőn jeleníti meg a program, 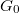 mértékegységben. Az adatok mintavételezése 100 kHz frekvenciával történik, vagyis két egymást követő adatpont között
mértékegységben. Az adatok mintavételezése 100 kHz frekvenciával történik, vagyis két egymást követő adatpont között 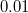 ms idő telik el.
ms idő telik el.
A Trigger funkciót használva az összes mért adat közül kiválaszthatjuk a számunkra érdekes adatpontokat. Ehhez meg kell adni egy vezetőképességszintet, egy feltételt (a trigger szint felett vagy az alatt kezdje a program az adatok megjelenítését), valamint azt, hogy hány pontot ábrázoljon a program a feltétel teljesülése előtt illetve után. A program csak azokat az adatpontokat menti el az induláskor kiválasztott fájlba, amelyeket a Trigger funkciót bekapcsolva megjelenít a felső kijelzőn. Bármelyik másik kijelzőn megjelenített adatokat is elmenthetjük a következő módon: jobb egérgombbal klikk a kijelzőre, a legördülő menüből válaszzuk ki az Export menüpontot, azon belül az Export Data to Clipboard-ra kattintva az adatokat vágólapra helyezhetjük, vagy az Export Data to Excel-re kattintva MS Excel-el elmenthetjük azokat.
A szakítás közben mért görbék kiértékelésének egyik alapvető eszköze a vezetőképesség-hisztogram, amit az alsó kijelző jelenít meg. Ezt úgy kapjuk, ha a szakítási görbék vezetőképesség-tengelyét felosztjuk egyenlő részekre, ún. bin-ekre, majd megszámoljuk, hogy az egyes bin-ekhez hány adatpont tartozik. Ezt elvégezve és összegezve akár több ezer görbére kaphatunk a 5/b. ábrához hasonló hisztogramot. A hisztogramon csúcsok jelzik azokat a vezetőképesség-értékeket, ahol a szakítási görbéken jellemzően platók jelennek meg.
A Clear gombot megnyomva törlődik az alsó kijelző tartalma valamint újraindul a hisztogram számítása. A Pause gombot megnyomva leállíthatjuk a mérést, így jobban megvizsgálható egy adott szakítási görbe. A kijelzők bal felső sarkában található eszközökkel ránagyíthatunk a mért görbék egyes szakaszára.
A Controller gombbal megnyithatjuk a szabályozást végző ablakot (az ábrán középen), valamint a Motor gombbal a léptető motort vezérlő ablakot (az ábra jobb oldalán).
A motort vezérlő ablakban a Forward illetve Backward gombok lenyomásakor a motor a megfelelő irányba kezd el lépegetni. A Delay vezérlőben állíthatjuk be, hogy két lépés között hány ms ideig várakozzon.
A Controller ablakot a szabályozás feladathoz használhatjuk. Fontos, hogy itt is újra be kell állítani a mintára adott feszültséget valamint az erősítés mértékét. A P illetve Ti vezérlőkben állíthatjuk be a szabályozás paramétereit. A felső kijelző vagy a vezetőképességet vagy a hibajelet (SetPoint és az éppen aktuálisan mért vezetőképesség különbsége) ábrázolhatjuk. A kontaktus vezetőképességét 1 kHz frekvenciával mintavételezi a program, azonban a piezo-t vezérlő kimenetet csak 100 Hz-el frissíti. Az alsó kijelzőn a szabályozó jel, vagyis piezo-ra kapcsolt feszültség látható.
A méréshez használt eszközök
- Minta:
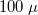 m átmérőjű arany szál középen bevágott lapkára forrasztva
m átmérőjű arany szál középen bevágott lapkára forrasztva
- Mintatartó piezomozgatóval valamint léptetőmotorral felszerelve
- motor tápegység
- NI myDAQ adatgyűjtő kártya
- Próbapanel
- TL081 műveleti erősítő x2
- Elenállások:
- 100 Ohm
- 330 Ohm x2
- 2.5 kOhm
- 10 kOhm
- 100 kOhm
- 1 MOhm
- kábelek:
- piezo-hoz
- próbapanelhez
- motorhoz
- mintához
- PC mérésvezérlő szoftverrel