Próbalap szupra

A szupravezetés elmélete dióhéjban

Heike Kamerlingh Onnes holland fizikus, miután 1911-ben megépítette hélium cseppfolyósító berendezését, elsőként végezhetett kísérleteket az abszolút nulla fokhoz igazán közeli hőmérsékleteken. Alacsony hőmérsékleti mérései pár hónapon belül nagyon meghökkentő felfedezéshez vezettek: azt találta, hogy egy higanyszál ellenállása 4,19 K hőmérséklet alatt zérusra csökken. Később kiderült, hogy számos anyag (pl. ólom, ón, alumínium) tökéletes vezetőként, úgynevezett szupvavezetőként viselkedik megfelelően alacsony hőmérsékleten. Kammerling Onnes munkáját már két évvel később, 1913-ban Nobel-díjjal jutalmazták.

A szupravezetés felfedezését követően közel fél évszázadot kellett várni a jelenség elméletének megszületésére (J. Bardeen, L. Cooper, R. Schiffer – 1957, Nobel-díj: 1972). Eszerint a szupravezető áramot szállító töltések különös tulajdonságokkal rendelkező elektron-párok, amelyek az egyszerű elektronoktól eltérő módon terjednek egy kristályban. Az ún. Cooper-párok viselkedésének kísérleti vizsgálata (Nobel-díj: 1973) vezetett a későbbiekben olyan alkalmazási lehetőségekre, mint a legérzékenyebb mágneses tér szenzor (SQUID) megalkotása, a világ leggyorsabb “hagyományos” számítógépeinek készítése, vagy a szupravezető nanoszerkezeteken alapuló kvantum-számítógépek perspektívája.

Onnes korai felfedezése óta a szupravezetés folyamatosan a modern fizika kiemelt témái közé tartozik. Ezt jelzi, hogy szupravezetéssel kapcsolatos elméleti vagy kísérleti munkákért a fentieken kívül 1987-ben és 2003-ban is osztottak ki Nobel-díjakat. Kiemelkedő technikai jelentőségű a magashőmérsékletű szupravezetőkért odaítélt Nobel-díj (1987), hiszen ekkor vált lehetővé, hogy a folyékony héliumnál lényegesen olcsóbb folyékony nitrogen forráspontján is elérhető legyen a szupravezetés. A magashőmérsékletű szupravezetéshez kapcsolódó elméleti modellekért 2003-ban ítéltek oda újabb Nobel-díjat. Az ilyen új anyagok kedvező tulajdonságai révén olyan lehetőségek is ígéretessé váltak, mint szupravezető motorok vagy távvezetékek készítése.

A szupravezető állapotban tapasztalt nulla elektromos ellenállás lehetővé teszi, hogy egy szupravezető tekercsbe áramot vezetve, majd a tápegységet kiiktatva és a tekercs végeit rövidre zárva a tekercsben keringő, akár 100 Amperes nagyságú, időben nem csillapodó áramokkal több Tesla nagyságú mágneses tereket tartsunk fenn további külső meghajtás nélkül. Napjainkban ezt az elvet használják ki a mágnesesen lebegtetett vonatok, az orvosi MRI készülékek vagy a CERN részecskegyorsító szupravezető mágneseiben.

A szupravezetés másik kísérő jelensége az 1933-ban felfedezett ún. Meissner-effektus. Meissner és Ochsenfeld megmutatták, hogy egy kritikus érték alatt a mágneses tér nem tud behatolni a szupravezetők belsejébe, valamint a véges mágneses térben lehűtött és szupravezetővé vált anyagok az átalakulási hőmérsékletük alá hűtve kiszorítják magukból a mágneses teret. Míg az előbbi tulajdonság önmagában megmagyarázható az időben változó külső mágneses tér által keltett, és a szupravezetők nulla elektromos ellenállása miatt nem csillapodó köráramok következtében fellépő kompenzáló mágneses térrel, az utóbbi jelenség túlmutat a klasszikus elektrodinamika keretein. Az elméletet egy szupravezető gyűrűre alkalmazva azt várjuk, hogy a szupravezető állapotban, a gyűrű síkjára merőlegesen bekapcsolt mágneses tér a gyűrű belsejébe nem hatol be. Ezzel szemben a mágneses térben lehűtött szupravezető gyűrű belsejében a külső tér lekapcsolása után is bent marad, “befagy” a mágneses tér.

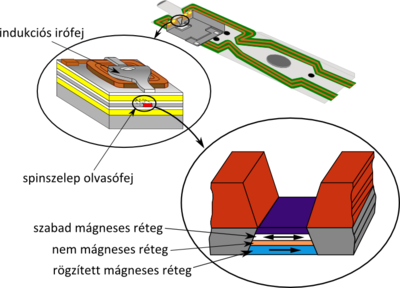
1. ábra. Az óriás mágneses ellenállás elvén alapuló merevlemezek működése.

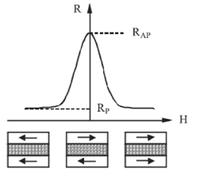
A szupravezető gyűrű belsejében felépülő vagy onnan kiszoruló mágneses teret a merevlemezek olvasófejeiben is alkalmazott mágneses tér érzékelő szenzorral mérhetjük. Az ilyen, ún. óriás mágneses ellenállást (GMR) mutató nanoszerkezetek felfedezése (1988) Albert Fert és Peter Grünberg nevéhez kötődik, akik 2007-ben Nobel-díjat kaptak felfedezésükért. A szerkezet két ferromágneses rétegből áll, amelyeket egy vékony nemmágneses réteg választ el egymástól (lásd 1. ábra). A felhasznált anyagok és a nemmágneses réteg vastagságának megfelelő megválasztásával elérhető, hogy külső mágneses tér hiányában a két réteg mágnesezettsége egymással ellentétes irányú legyen. Erre az elrendezésre megfelelő nagyságú külső mágneses teret kapcsolva a két réteg mágnesezettségét beforgathatjuk egymással párhuzamos irányba. A mágnesezettség párhuzamos (parallel, P) állása esetén a 2. ábrán mutatott elrendezés ellenállása lényegesen kisebb, mint az ellentétes (antiparallel, AP) beállás esetén, így külső mágneses tér alkalmazásával jelentős ellenállás-csökkenést tudunk elérni. Ezt a jelenséget hívjuk óriás mágneses ellenállásnak.

2. ábra. Az óriás mágneses ellenállás szemléltetése.

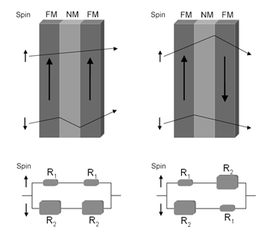
A jelenséget a következő egyszerű modellel szemléltethetjük: Bontsuk fel az elektromos áramot “fel” illetve “le” spinű elektronok áramára. A le spinű elektronok egy felfelé álló mágnesezettségű rétegen lényegesen nehezebben haladnak át, mint egy lefelé álló mágnesezettségűn. Jelöljük egy mágneses réteg ellenállását egy bizonyos spinű elektronokra nézve -el ha a réteg mágnesezettségi iránya megegyezik az elektronok spinirányával, illetve -vel, ha a mágnesezettség iránya ellentétes az elektronok spinirányával. A fel és le spinű elektronokat független áramcsatornaként kezelve a parallel és antiparallel mágnesezettségű rétegek eredő ellenállása a 3. ábrán szemléltetett helyettesítő képpel modellezhető.

3. ábra. Különböző mágnesezettségű rétegek eredő ellenállásának számolsására szolgáló helyettesítő kép.

A fenti két ellenállást 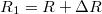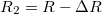$\setbox0\hbox{$ R_1 = R + \Delta R $}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$ R_2 = R - \Delta R $}% \message{//depth:\the\dp0//}% \box0%$ alakban kifejezve a parallel és antiparallel beállások esetén az ellenállás 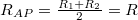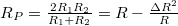$\setbox0\hbox{$ R_{AP} = \frac{R_1 + R_2}{2} = R$}% \message{//depth:\the\dp0//}% \box0%$, $\setbox0\hbox{$R_{P}=\frac{2R_1 R_2}{R_1 + R_2}=R-\frac{\Delta R^2}{R}$}% \message{//depth:\the\dp0//}% \box0%$ , azaz a P elrendezés ellenállása valóban kisebb, mint az AP elrendezésé.

Az elektronikai iparban a mágneses ellenálláson alapuló technológiák első és máig is legjelentősebb felhasználása a merevlemezek olvasófejéhez kapcsolódik. Ezekben az 1990-es évek elején induktív olvasófejeket alkalmaztak: a merevlemezeken mágnesesen tárolt információ kiolvasását a gyorsan forgó mágneses lemez által egy kis tekercsben indukált feszültség segítségével végezték. Az 1990-es évek közepén áttérve a magnetorezisztív technológiára először az anizotróp mágneses ellenálláson (AMR) alapuló olvasófejek terjedtek el. Az AMR fejeknek köszönhetően jelentős tárolókapacitás-növekedést sikerült elérni, azonban az AMR jelenség kis, <1 százalékos ellenállás-változása a későbbiekben komoly korlátozó tényezővé vált. A GMR jelensége ezt az értéket egy nagyságrenddel meghaladja, így az 1990-es évek vége óta a merevlemezekben a GMR jelenségén alapuló olvasófejeket használnak. Ezzel a módszerrel a merevlemezek tárolókapacitásának további jelentős növekedését lehetett elérni.

A GMR olvasófejek az ún. spin-szelep elrendezést követik. A két mágneses rétegből az egyik rögzített, nehezen elfordítható irányú mágnesezettséggel rendelkezik, míg a másik egy könnyen forgatható mágnesezettségű réteg. Az utóbbi réteg mágnesezettsége az olvasófej alatt forgó merevlemezen tárolt bitek mágnesezési irányának megfelelően áll be, így az információ a spinszelep ellenállásának mérésével egyszerűen kiolvasható.

Mérési feladatok

Biztonsági előírások:

• A mérések során fokozott óvatossággal kezeljétek a szupravezető mintákat, mivel drága és sérülékeny eszközök.
• A szupravezető anyagok mérgezőek az emberi szervezet számára, így a mérés során ne egyetek, valamint a mérések végén mossatok kezet. A szupravezető minták felületén speciális bevonat van, így szabad kézzel megfogva sem kerül szennyeződés a kezetekre, azonban fontos az elővigyázatosság.
• A folyékony nitrogénnel óvatosan bánjatok, kerüljétek azt, hogy a bőrötökhöz érjen. Semmiképp se mártsátok bele a kezeteket, és ne igyatok belőle!

Szupravezető fázisátalakulásának mérése

1. Állítsátok össze a 4. ábrán látható mérési elrendezést!

4. ábra. Szupravezető pálca átalakulásának mérésére szolgáló elrendezés.

Az összeállítás lépései:

• Csatlakoztassátok a mérőkártyát egy USB kábelen keresztül a számítógépre.
• A minta négypontellenállásának mérésére szolgáló banándugók közül a V+ és V- kivezetéseket csatlakoztassátok a mérőkártya multiméter bemeneteire, az I+ és I- kivezetéseket pedig a 100 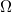$\setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%$ ellenállással sorban a DGND és az 5 V kimenetekre. A kábel és az ellenállás összekapcsolásában segít a sorkapocs.
• A hőmérsékletmérésre szolgáló kábelek közül a fekete színűeket egy 1 k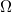$\setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%$ ellenállással sorban kössétek az AO0 és az AGND kivezetésekre, a másik kettőt az AI 0+ és 0- bemenetekre.

2. Indítsátok el a mérésvezérlő programot! Ehhez a …./myDAQprogram.sln filet kell megnyitni.

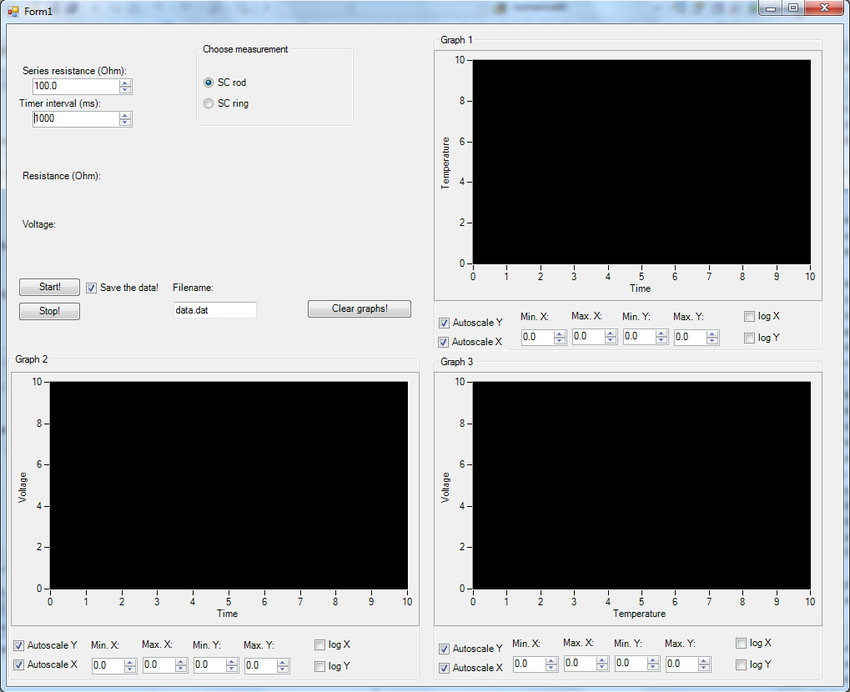
5. ábra. A mérésvezérlő program kezelőfelülete.

A program kezelőfelülete az 5. ábrán látható. Az „SC rod” és „SC ring” opciókkal tudtok váltani a szupravezető pálca és gyűrű mérései között. Először az „SC rod” opcióra lesz szükségetek. A Start! gomb megnyomásával indíthatjátok a mérést, és a Stop! gombbal állíthatjátok le. A mérési adatokat a Filename szövegdobozban megadott néven tudjátok elmenteni. A mentés idejére állítsátok meg a mérést. Ha új mérést kezdtek, a Clear graphs! gombra kattintva tudjátok törölni a grafikonok adatait.

A program a hőmérőn és a soros ellenálláson, valamint csak a hőmérőn eső feszültségértékekből számolja ki a PT1000 típusú hőmérő ellenállását. Ennek a hőmérőnek működési elve a következő: szobahőmérsékleten 1 k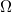$\setbox0\hbox{$\Omega$}% \message{//depth:\the\dp0//}% \box0%$ az ellenállása, amely csökkenő hőmérséklet mellett csökken, növekvő mellett nő. -50 °C és 200 °C között jó közelítéssel lineáris az ellenállás-hőmérséklet összefüggése, ezen egyenes alapján számolja ki a mérésvezérlő program az aktuális hőmérsékletet. Alacsony hőmérsékleten ez már nem feltétlen teljesül, így a folyékony nitrogén hőmérsékletén (77 K= -196 °C) ez a közelítés némi pontatlanságot visz a mérésbe.

Ha mindennel elkészültetek, szóljatok a mérésvezetőnek, aki ellenőrzi az összeállítást és kitölti nektek a folyékony nitrogént.

3. A mérésvezérlő program segítségével vegyétek fel a szupravezető minta négypontellenállásának hőmérsékletfüggését úgy, hogy lassan belemártjátok a mintatartót a folyékony nitrogénbe. Miután stabilizálódott a hőmérséklet a folyékony nitrogén hőmérsékletén, lassan emeljétek ki a mintatartót és az asztalra téve várjátok meg, amíg felmelegszik szobahőmérsékletre. Melegedés közben is mérjétek az ellenállás hőmérsékletfüggését. A mért görbék alapján határozzátok meg a szupravezető átalakuláshoz tartozó kritikus hőmérsékletet!

• Miért térnek el a hűléskor és a melegedéskor mért átalakulási hőmérsékletek egymástól?
• Milyen hibái lehetnek a hőmérséklet mérésének?
• Mekkora hibával tudjuk meghatározni a minta ellenállását? Mekkora az a legnagyobb ellenállás, amit még nullának mérünk?

Meissner - effektus tanulmányozása

1. Állítsátok össze a mérési elrendezést a 6. ábra alapján!

6. ábra Szupravezető gyűrű vizsgálatának mérési elrendezése

Ennek menete:

• A mérőkártyáról válasszátok le az előző mérés eszközeit.
• A mágneses szenzor kék/barna kivezetését csatlakoztassátok a mérőkártya 5 V kimenetére, a kék-fehér/barna-fehér kivezetést a DGND kimenetre.
• A szenzor zöld/narancs és zöld-fehér/narancs-fehér kivezetéseit banándugókkal csatlakoztassátok a multiméter bemenetre.
• A táp kivezetéseit banánkábelekkel kössétek a tekercsre.
• A mérésvezérlő programban válasszátok az „SC ring” opciót.

2. Számoljátok ki, hogy mekkora lehet a mágneses tér a tekercs közepén a tekercsen eső feszültség függvényében! A tekercs menetszáma és ellenállása a tekercs oldalán olvasható, a hosszát tolómérővel mérhetitek meg.

Ha ezzel elkészültetek, szóljatok a mérésvezetőnek, aki ellenőrzi az összeállítást és a számolásotokat.

3. Kalibráljátok a GMR szenzort szobahőmérsékleten! Ehhez helyezzétek a szenzort a tekercs középtengelyébe, és folyamatosan emeljétek a tekercsen eső feszültséget, valamint mérjétek a szenzor feszültségét a mérésvezérlő program segítségével. Az előző feladatban levezetett képlet alapján meg tudjátok határozni, hogy a GMR szenzoron mért feszültség mekkora mágneses térnek felel meg. Érdemes egy excel táblázatba importálni a mért adatokat, és egy új oszlopban kiszámolni a szenzor feszültségéhez tartozó mágneses tér értékeket. Érdemes továbbá már itt is használni a hungarocell edényt, és annak aljára helyezni a szenzort, hogy a mérések során mindig ugyan abban a pozícióban legyen.

4. Kalibráljátok a GMR szenzort folyékony nitrogénben! Az előző feladatot végezzétek el úgy is, hogy a tekercs közepébe helyezitek a szögletes hungarocell edényt, amibe töltsetek folyékony nitrogént. Ebben merítsétek a GMR szenzort.

5. Vegyétek ki a GMR szenzort az edényből, kapcsoljátok le a mágneses teret és a műanyag csipesz segítségével helyezzétek a szupravezető gyűrűt az edény aljára. Ha szükséges, töltsetek még folyékony nitrogént az edénybe. Ezután helyezzétek a GMR szenzort a gyűrű közepébe, és kapcsoljatok a tekercsre körülbelül 3.5mT mágneses térnek megfelelő feszültséget. Mit mutat a szenzor?

• Mi az oka a jelenségnek?

6. Vegyétek ki a szenzort és a gyűrűt az edényből, utóbbihoz használjátok a műanyag csipeszt. Várjátok meg, míg a gyűrű felmelegedik, közben öntsétek vissza az edényből a folyékony nitrogént a termoszba. Ezután helyezzétek vissza az üres edényt és a mintát a tekercs közepére, majd kapcsoljatok a tekercsre ismét 3.5mT mágneses térnek megfelelő feszültséget. Öntsetek óvatosan folyékony nitrogént az edénybe, és helyezzétek vissza a mágneses szenzort. Kapcsoljátok le a tekercs által biztosított külső mágneses teret. A kikapcsolás pillanatától számítva az idő függvényében mérjétek a szenzor jelét legalább 10 percen keresztül! Közben ha szükséges, pótoljátok a folyékony nitrogént.

• Kikapcsoltuk a külső mágneses teret, mégsem mutat zérus térértéket a szenzor. Miért van ez?
• A mérés alapján adjatok felső becslést a gyűrű ellenállására!
• Az előző feladatrészben számolt zérus ellenállás hibájával kalkulálva mennyi idő alatt csökken le a gyűrűben a mágneses tér nullára?

Függelék: A mérésen használt eszközök

• szupravezető pálca
• mintatartó hőmérővel
• myDAQ mérőkártya
• termosz
• folyékony nitrogén
• szupravezető gyűrű
• hungarocell edény
• tekercs
• mágneses szenzor
• műanyag csipesz
• tápegység
• banán kábelek
• csavarhúzó
• tolómérő