„Próbalap” változatai közötti eltérés
(→Nobel-díjas fizika mindennapi alkalmazásban - szupravezetés) |
|||
| (egy szerkesztő 22 közbeeső változata nincs mutatva) | |||
| 1. sor: | 1. sor: | ||
| − | + | A nanotechnológia jelentősen hozzájárult az elektronika fejlődéséhez. Gordon E. Moore, az Intel cég egyik alapítója 1965-ben azt a megfigyelését tette közzé, miszerint egy integrált áramkörben lévő tranzisztorok száma két évenként megduplázódik. Ez a megfigyelés egészen napjainkig teljesülni látszik, ennek megfelelően a tranzisztorok mérete szintén exponenciálisan csökkent az elmúlt évtizedekben (1. ábra). Manapság egy tranzisztor aktív tartománya mindössze ~10 nm széles. Ez a méret elméletileg még két nagyságrenddel csökkenthető, amíg elérjük az elképzelhető legkisebb, egyetlen atomból álló tranzisztorokat. A további méretcsökkentés azonban számtalan technológiai problémát vet fel, így a jelenleginél kisebb, vagy más működési elvet követő információtárolási és feldolgozási technológiák kidolgozása világszerte intenzív kutatások tárgyát képezi. Ennek megfelelően a nanofizikai kutatások túlmutatnak az érdekes jelenségek feltérképezésén, és alapvetően hozzájárulnak a jövő technológiáinak kidolgozásához. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| + | |- | ||
| + | | [[Fájl:Moore.png|közép|400px|]] | ||
| + | |- | ||
| + | | align="center"|1. ábra. ''Tipikus méretskálák és a DRAM generációk exponenciális méretcsökkenését szemléltető Moore-törvény.'' | ||
| + | |} | ||
| − | + | A következőkben rövid betekintést nyújtunk a nanoáramkörök illetve különböző nanoszerkezetek készítésének és vizsgálatának eszköztárába. | |
| − | + | == Pásztázó alagútmikroszkóp (Scanning Tunneling Microscope - STM) == | |
| − | + | <wlatex> | |
| + | Már az ókori görögök is azt feltételezték, hogy az anyag atomokból épül fel. Ezt a feltételezést a 20. század elején számos kísérlettel sikerült bizonyítani, azonban ahhoz, hogy képet tudjunk készíteni egy anyag felületén lévő atomokról egészen 1981-ig kellett várni, amikor is Gerd Binnig és Heinrich Rohrer megépítették az első pásztázó alagútmikroszkópot. Találmányukért fizikai Nobel-díjat kaptak 1986-ban. Azóta az alagútmikroszkóp széleskörben elterjedt, manapság a nanofizikai kutatások egyik alapvető vizsgálati eszközei közé tartozik. | ||
| − | + | Működésének elve az alagúteffektuson alapul: egy hegyes tűt nm-es távolságra pozícionálunk a vizsgált minta felületéhez, a tűre feszültséget kapcsolunk, ennek hatására alagútáram folyik a tű és a minta között: | |
| − | + | $$I \propto V_b \cdot \mathrm{Exp}\left\{-A\cdot d\cdot \sqrt{\Phi} \right\},$$ | |
| − | + | ||
| − | { | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ahol $V_b$ a tű és a minta közé kapcsolt feszültség, $d$ a minta-tű távolság, $\Phi$ a kilépési munka valamint $A=1.025\;\mathrm{\AA\;}^{-1}eV^{-1/2}$ egy állandó. Az alagútáram exponenciális függése a minta-tű távolságtól rendkívül pontos mérést tesz lehetővé: ha mindössze $1\;\AA$-el, azaz körülbelül fél atomnyi távolsággal, megnöveljük a minta-tű távolságot, az áram a tizedére csökken. | |
| − | |||
| − | [[ | + | {| cellpadding="5" cellspacing="0" align="center" |
| + | |- | ||
| + | | [[Fájl:STM_approach.ogv|bélyegkép|közép|800px|thumbtime=0:08]] | ||
| + | |- | ||
| + | | align="center"|2. ábra. ''STM tű közelítése a felülethez, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.'' | ||
| + | |} | ||
| − | + | A mérés kezdetén a 2. ábrán látható módon addig közelítjük a tűt a minta felületéhez, míg az alagútáram el nem éri a - tipikusan $nA$-es nagyságrendű - kívánt értéket. Alagútmikroszkóppal két különböző módon végezhetünk méréseket. A konstans áram üzemmódot használják leggyakrabban (3. ábra), ehhez a minta felületével párhuzamosan pásztázunk a tűvel miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest. Ilyen módon akár atomi felbontással letapogatható a minta topográfiája. | |
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| + | |- | ||
| + | | [[Fájl:STM_feedback.ogv|bélyegkép|közép|800px|thumbtime=0:17]] | ||
| + | |- | ||
| + | | align="center"|3. ábra. ''Pásztázás a minta felett: topográfia felvétele konstans áram üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.'' | ||
| + | |} | ||
| − | + | A másik üzemmód a konstans magasság üzemmód (4. ábra), ehhez a szabályozást kikapcsolva, a tűt állandó magasságban tartva pásztázunk a felület felett. A mért alagútáramból meghatározható a minta topográfiája. Ez az üzemmód gyors pásztázási sebességet tesz lehetővé, ami többek között akkor lehet hasznos, ha valamilyen lassú időbeli változást - például hőtágulás miatti csúszást - kell kiküszöbölni. Ahhoz, hogy ezt a mérési módot alkalmazhassuk, a mintának kellőképpen simának kell lennie és a tűt elegendően távol kell tartanunk, hogy ne ütközzön a felületbe. | |
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| + | |- | ||
| + | | [[Fájl:STM_scan_noFeedback.ogv|bélyegkép|közép|800px|thumbtime=0:07]] | ||
| + | |- | ||
| + | | align="center"|4. ábra. ''Pásztázás a minta felett: topográfia felvétele konstans magasság üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013.'' | ||
| + | |} | ||
| − | + | Az alagútáram exponenciális távolságfüggése lehetővé teszi, hogy akár egy ollóval hegyezett tűvel is készíthetünk jó minőségű STM képet. Az alábbi ábrák egy grafit minta felületének valamint egy szén nanocsőnek az atomi felbontású képét mutatják be. | |
| − | + | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:HOPG_atomic.png|közép|500px]] | ||
| + | |- | ||
| + | | align="center"|5. ábra. ''Atomi felbontású STM kép grafit minta felületéről, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013.'' | ||
|} | |} | ||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | [[Fájl:Chiraltube.gif|közép|300px]] | ||
| + | |- | ||
| + | | align="center"|6. ábra. ''Szén nanocső atomi felbontású képe, forrás: [http://en.wikipedia.org/wiki/File:Chiraltube.gif Wikipedia]'' | ||
| + | |} | ||
| − | |||
| − | + | Az STM tű nem csak a képalkotásra, hanem a minta felületének atomi felbontású manipulációjára is alkalmas: a tű segítségével atomokat lehet mozgatni a felületen. Ezzel a technikával hozták létre a 7. ábrán látható kör alakzatot, amit 48 vas atom alkot egy réz felületen. Az alagútmikroszkópos felvételen jól megfigyelhetőek a kör belsejében kialakuló állóhullámok ("Quantum corral"). | |
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| − | {| | + | |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | + | | [[Fájl:Quantum_corral.jpg|közép|300px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | align="center"|7. ábra. ''Elektron-állóhullámok egy atomokból kirakott kör belsejében, forrás: [http://en.wikipedia.org/wiki/File:The_Well_(Quantum_Corral).jpg Wikipedia]'' |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| + | |||
| + | Egy másik, hasonló kísérlet során 36 kobalt atomból álló ellipszist hoztak létre, aminek az egyik fókuszpontjába egy kobalt atomot helyeztek. Az elektronok hullámtermészetének köszönhetően az ellipszis másik fókuszpontjában is mérhető a kobalt atom hatása.<sup> [http://www.nature.com/nature/journal/v403/n6769/abs/403512a0.html 1]</sup> | ||
| + | |||
| + | Az STM legnagyobb hátránya, hogy csak elektromosan vezető felületeket vizsgálhatunk vele. Szigetelő felületek vizsgálatára fejlesztették ki az atomerő mikroszkópot. | ||
| + | </wlatex> | ||
| + | ==Önszerveződő nanoszerkezetek== | ||
| + | <wlatex> | ||
| + | * A felületek gyakran átrendeződnek jól definiált struktúrájú alakzatokba (surface reconstruction) | ||
| + | * Molekulákból önszerveződő rétegeket képezhetünk. Pl. arany felületre a tiol csoport (SH) szeret kötődni, így egyik végükön tiol csoporttal rendelkező molekulák egy arany felületen önszerveződő monoréteget (self-assambled monolayer, SAM) alkothatnak | ||
| + | * Grafén nanoszalagok létrehozása oxidációval. SiO2 hordozón elhelyezett grafén réteget először oxigén légkörben oxidálunk (~500 OC), aminek hatására kör alakú lyukak jönnek létre. Ezeket 700 OC-os argon atmoszférában hőkezeljük, miközben jól definiált irányú hatszögek jönnek létre. (Reakció: SiO2+C -> SiO + CO) Forrás: Magda Gábor, Dr. Bíró László Péter (MFA) | ||
| + | * Bizonyos anyagok szakítás során szeretnek atomi láncokat képezni | ||
| + | |||
| + | Néhány atomból álló kontaktusok vizsgálata: | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | | + | | align="center"|[[Fájl:histogram.jpg|közép|500px]] |
| − | + | ||
|- | |- | ||
| − | | | + | | align="center"|22/a. ábra. ''Atomi láncképződés.'' |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | {| cellpadding="5" cellspacing="0" align="center" | |
| − | | | + | |
|- | |- | ||
| − | | | + | | align="center"|[[Fájl:chain.ogv|közép|150px|thumbtime=0:01]] |
| − | + | ||
|- | |- | ||
| − | | | + | | align="center"|22/a. ábra. ''Atomi láncképződés.'' |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Az atomi kontaktusok vizsgálatára alkalmas mérőberendezések egyike az úgynevezett MCBJ technika (Mechanically Controllable Break Junction technique), melynek felépítése a 3/a. ábrán látható. Egy középen elvékonyított fémszálat két ragasztópötty rögzít egy rugalmas lapkára, amit egy piezo mozgatóval meghajlítunk, így a vezeték két rögzített pontja távolodik egymástól. Már magát a piezo mozgatását is nm alatti pontossággal végezhetjük, a berendezés geometriájából eredő mechanikai áttételnek köszönhetően a szétszakítandó vezeték végeinek elmozdulása a piezo mozgásánál körülbelül két nagyságrenddel kisebb. Így a közvetlenül a szakadás előtt kialakuló atomi kontaktusok vizsgálatára kiemelkedő mechnaikai stabilitás mellett nyílik lehetőség. Miután a minta teljesen elszakadt, újra közelíteni kezdjük a vezetékek végeit, a kontaktus újra felépül. Így egy mintával akár több ezer szakítási görbe is felvehető. | |
| − | | | + | |
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | | + | | align="center"|[[Fájl:MCBJ.png|közép|300px|]] |
| − | + | | align="center"|[[Fájl:MCBJ_gold.jpg|közép|350px|]] | |
|- | |- | ||
| − | | | + | | align="center"|20/a. ábra. ''MCBJ elrendezés vázlata, forrás: Halbritter András PhD dolgozat, 2003.'' |
| − | | | + | | align="center"|20/b. ábra. ''Arany vezeték szakítása közben mért vezetőképesség görbék.'' |
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A szakítás közben, amikor a vezeték legkisebb keresztmetszetében már csak néhány atom található, a kontaktus vezetőképessége lépcsőzetesen változik (3/b. ábra). Ez a viselkedés elsősorban az anyag atomi felépítésével magyarázható, de az elektronok kvantummechanikai viselkedése is fontos szerepet játszik [hivatkozás a nanovezetékek fejezetre]. A széthúzás közben egy adott atomi konfigurációt először rugalmasan deformálunk, ilyenkor a vezetőképesség nem változik jelentősen. A vezetéket tovább nyújtva egy hirtelen | |
| − | | | + | atomi átrendeződést figyelhetünk meg, ami a vezetőképesség ugrásszerű változását eredményezi. A teljes szétszakadás előtti utolsó plató a legtöbb esetben egy olyan kontaktushoz tartozik, melyben a két elektródát egyetlen atom köti össze. Bizonyos anyagok esetén (például: Au, Cu, Ag) az utolsó platóhoz tartozó vezetőképesség jól reprodukálóan az úgynevezett vezetőképesség kvantummal - egy univerzális állandóval - egyezik meg: $1 G_0 = \frac{2 e^2}{h}\approx 1/12900\Omega$-nak megfelelő értéket vesz fel. |
| + | |||
| + | A szakításkor bekövetkező atomi átrendeződések véletlenszerűek, ezért a mért vezetőképesség görbék különbözőek lehetnek, ennek ellenére megfigyelhetőek bizonyos hasonlóságok. Az egyes konfigurációkhoz tartozó platók mindig közel azonos vezetőképességnél találhatóak, azonban ez csak sok - akár több ezer - görbe összehasonlításakor lesz látható. Erre a célra az egyik alapvető kiértékelési mód a mért vezetőképesség görbék hisztogramjának számítása: a hisztogramban csúcsok jelennek azoknál a vezetőképesség értékeknél, ahol a mért vezetőképesség görbékben platók figyelhetőek meg. A hisztogram csúcsai mindig ugyanazokon – a minta anyagára jellemző – vezetőképesség értéknél jelennek meg. | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
|- | |- | ||
| − | | | + | | align="center"|[[Fájl:MCBJ_hist.ogv|közép|380px|thumbtime=0:01]] |
| − | + | | align="center"|[[Fájl:MCBJ_hist_molecule.ogv|közép|210px|thumbtime=0:01]] | |
|- | |- | ||
| − | | | + | | align="center"|21/a. ábra. ''Vezetőképesség hisztogram készítése az egyedi mért vezetőképesség görbékből.'' |
| − | | | + | | align="center"|21/b. ábra. ''A kontaktusba molekula épül be - a hisztogramban új csúcs jelenik meg.'' |
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Az MCBJ mérés felhasználható arra is, hogy egyedi molekulák vezetőképességét vizsgáljuk. Ehhez a vezeték folyamatos széthúzása majd összenyomása közben molekulákat juttatunk a kontaktushoz, melyek képesek beépülni a két elektróda közé. A beépült molekula következtében megváltozik a kontaktus vezetőképessége, a mért görbék hisztogramjában egy új csúcs jelenik meg (21/b. ábra). A csúcs helye a beépült molekula vezetőképességét jellemzi. | |
| − | | | + | |
| + | Bizonyos anyagokkal, speciális körülmények között mérve (például arany minta alacsony hőmérsékleten) érdekes jelenség figyelhető meg: az egyedi görbéken megfigyelhető, hogy széthúzáskor az utolsó plató sokszor lényegesen hosszabb a többi platónál. Ez azzal magyarázható, hogy az egyatomos kontaktust széthúzva az nem feltétlenül szakad el egyből, helyette egy több atomból álló atomlánc „húzódik” a két elektróda között. Az atomi láncképződést az utoló plató hosszának statisztikai vizsgálatával lehet kimutatni, a lánc hosszúsága a vezetőképességben mért plató hosszúságával jellemezhető. | ||
| + | |||
| + | {| cellpadding="5" cellspacing="0" align="center" | ||
| + | |- | ||
| + | | align="center"|[[Fájl:chain.ogv|közép|200px|thumbtime=0:01]] | ||
| + | | align="center"|[[Fájl:MCBJ_platolength.jpg|közép|350px|]] | ||
| + | |- | ||
| + | | align="center"|22/a. ábra. ''Atomi láncképződés.'' | ||
| + | | align="center"|22/b. ábra. ''Platóhosszúság hisztogram.'' | ||
|} | |} | ||
| − | + | Ha felrajzoljuk, hogy különböző platóhosszúságok milyen gyakorisággal fordulnak elő, akkor az így készített plató hosszúság hisztogramban csúcsok jelennek meg egyenlő | |
| − | + | távolságokra egymástól. A különböző csúcsok különböző számú atomból álló láncnak felelnek meg, a csúcsok közötti távolság – megfelelő kalibráció után – két szomszédos | |
| − | + | atom távolságát adja meg a láncban. | |
| − | + | ||
| − | + | [[Miért válassz minket? (szerkesztőlap)]] | |
| + | </wlatex> | ||
A lap jelenlegi, 2018. március 14., 13:20-kori változata
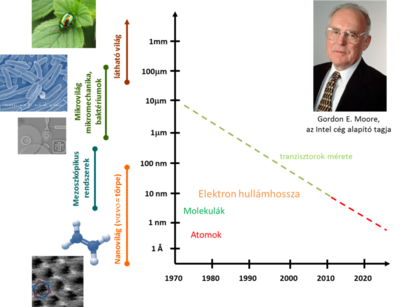
A nanotechnológia jelentősen hozzájárult az elektronika fejlődéséhez. Gordon E. Moore, az Intel cég egyik alapítója 1965-ben azt a megfigyelését tette közzé, miszerint egy integrált áramkörben lévő tranzisztorok száma két évenként megduplázódik. Ez a megfigyelés egészen napjainkig teljesülni látszik, ennek megfelelően a tranzisztorok mérete szintén exponenciálisan csökkent az elmúlt évtizedekben (1. ábra). Manapság egy tranzisztor aktív tartománya mindössze ~10 nm széles. Ez a méret elméletileg még két nagyságrenddel csökkenthető, amíg elérjük az elképzelhető legkisebb, egyetlen atomból álló tranzisztorokat. A további méretcsökkentés azonban számtalan technológiai problémát vet fel, így a jelenleginél kisebb, vagy más működési elvet követő információtárolási és feldolgozási technológiák kidolgozása világszerte intenzív kutatások tárgyát képezi. Ennek megfelelően a nanofizikai kutatások túlmutatnak az érdekes jelenségek feltérképezésén, és alapvetően hozzájárulnak a jövő technológiáinak kidolgozásához.
| 1. ábra. Tipikus méretskálák és a DRAM generációk exponenciális méretcsökkenését szemléltető Moore-törvény. |
A következőkben rövid betekintést nyújtunk a nanoáramkörök illetve különböző nanoszerkezetek készítésének és vizsgálatának eszköztárába.
[szerkesztés] Pásztázó alagútmikroszkóp (Scanning Tunneling Microscope - STM)
Már az ókori görögök is azt feltételezték, hogy az anyag atomokból épül fel. Ezt a feltételezést a 20. század elején számos kísérlettel sikerült bizonyítani, azonban ahhoz, hogy képet tudjunk készíteni egy anyag felületén lévő atomokról egészen 1981-ig kellett várni, amikor is Gerd Binnig és Heinrich Rohrer megépítették az első pásztázó alagútmikroszkópot. Találmányukért fizikai Nobel-díjat kaptak 1986-ban. Azóta az alagútmikroszkóp széleskörben elterjedt, manapság a nanofizikai kutatások egyik alapvető vizsgálati eszközei közé tartozik.
Működésének elve az alagúteffektuson alapul: egy hegyes tűt nm-es távolságra pozícionálunk a vizsgált minta felületéhez, a tűre feszültséget kapcsolunk, ennek hatására alagútáram folyik a tű és a minta között:
![\[I \propto V_b \cdot \mathrm{Exp}\left\{-A\cdot d\cdot \sqrt{\Phi} \right\},\]](/images/math/f/3/3/f33f7d155ad3c25c2642a7c71de1f639.png)
ahol 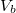 a tű és a minta közé kapcsolt feszültség,
a tű és a minta közé kapcsolt feszültség, 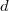 a minta-tű távolság,
a minta-tű távolság, 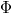 a kilépési munka valamint
a kilépési munka valamint 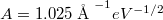 egy állandó. Az alagútáram exponenciális függése a minta-tű távolságtól rendkívül pontos mérést tesz lehetővé: ha mindössze
egy állandó. Az alagútáram exponenciális függése a minta-tű távolságtól rendkívül pontos mérést tesz lehetővé: ha mindössze 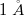 -el, azaz körülbelül fél atomnyi távolsággal, megnöveljük a minta-tű távolságot, az áram a tizedére csökken.
-el, azaz körülbelül fél atomnyi távolsággal, megnöveljük a minta-tű távolságot, az áram a tizedére csökken.
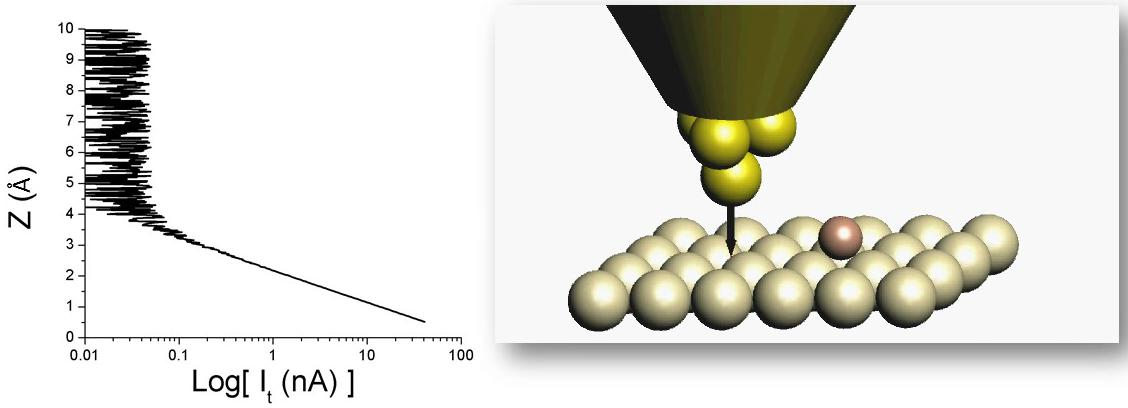
| 2. ábra. STM tű közelítése a felülethez, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
A mérés kezdetén a 2. ábrán látható módon addig közelítjük a tűt a minta felületéhez, míg az alagútáram el nem éri a - tipikusan 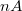 -es nagyságrendű - kívánt értéket. Alagútmikroszkóppal két különböző módon végezhetünk méréseket. A konstans áram üzemmódot használják leggyakrabban (3. ábra), ehhez a minta felületével párhuzamosan pásztázunk a tűvel miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest. Ilyen módon akár atomi felbontással letapogatható a minta topográfiája.
-es nagyságrendű - kívánt értéket. Alagútmikroszkóppal két különböző módon végezhetünk méréseket. A konstans áram üzemmódot használják leggyakrabban (3. ábra), ehhez a minta felületével párhuzamosan pásztázunk a tűvel miközben egy szabályozó áramkört használva úgy mozgatjuk a tűt a felületre merőleges irányban, hogy mindig állandó legyen a mért alagútáram, azaz a tű közel azonos távolságban mozogjon a minta felületéhez képest. Ilyen módon akár atomi felbontással letapogatható a minta topográfiája.
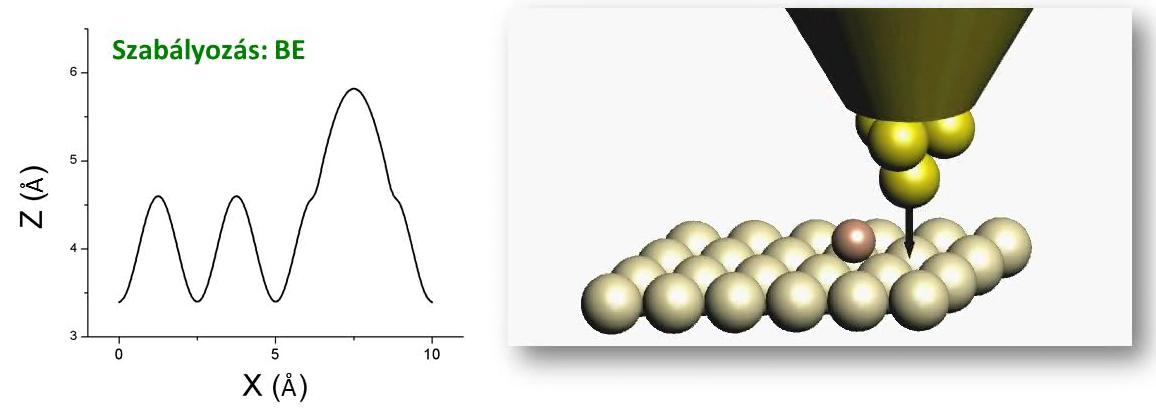
| 3. ábra. Pásztázás a minta felett: topográfia felvétele konstans áram üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
A másik üzemmód a konstans magasság üzemmód (4. ábra), ehhez a szabályozást kikapcsolva, a tűt állandó magasságban tartva pásztázunk a felület felett. A mért alagútáramból meghatározható a minta topográfiája. Ez az üzemmód gyors pásztázási sebességet tesz lehetővé, ami többek között akkor lehet hasznos, ha valamilyen lassú időbeli változást - például hőtágulás miatti csúszást - kell kiküszöbölni. Ahhoz, hogy ezt a mérési módot alkalmazhassuk, a mintának kellőképpen simának kell lennie és a tűt elegendően távol kell tartanunk, hogy ne ütközzön a felületbe.
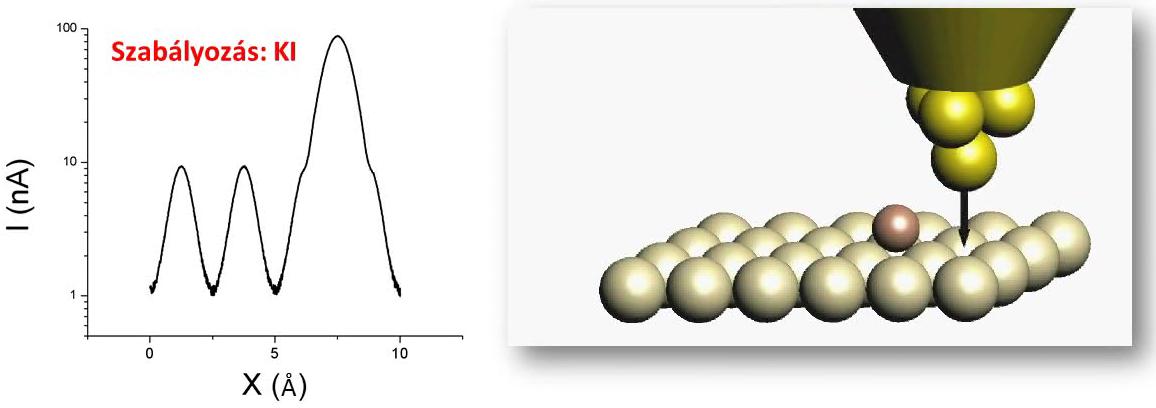
| 4. ábra. Pásztázás a minta felett: topográfia felvétele konstans magasság üzemmódban, forrás: Magyarkuti András diploma előadás, BME Fizika Tanszék, 2013. |
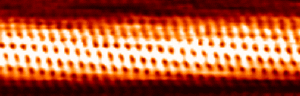
Az alagútáram exponenciális távolságfüggése lehetővé teszi, hogy akár egy ollóval hegyezett tűvel is készíthetünk jó minőségű STM képet. Az alábbi ábrák egy grafit minta felületének valamint egy szén nanocsőnek az atomi felbontású képét mutatják be.
| 5. ábra. Atomi felbontású STM kép grafit minta felületéről, forrás: Magyarkuti András diplomamunka, BME Fizika Tanszék, 2013. |
| 6. ábra. Szén nanocső atomi felbontású képe, forrás: Wikipedia |
Az STM tű nem csak a képalkotásra, hanem a minta felületének atomi felbontású manipulációjára is alkalmas: a tű segítségével atomokat lehet mozgatni a felületen. Ezzel a technikával hozták létre a 7. ábrán látható kör alakzatot, amit 48 vas atom alkot egy réz felületen. Az alagútmikroszkópos felvételen jól megfigyelhetőek a kör belsejében kialakuló állóhullámok ("Quantum corral").
| 7. ábra. Elektron-állóhullámok egy atomokból kirakott kör belsejében, forrás: Wikipedia |
Egy másik, hasonló kísérlet során 36 kobalt atomból álló ellipszist hoztak létre, aminek az egyik fókuszpontjába egy kobalt atomot helyeztek. Az elektronok hullámtermészetének köszönhetően az ellipszis másik fókuszpontjában is mérhető a kobalt atom hatása. 1
Az STM legnagyobb hátránya, hogy csak elektromosan vezető felületeket vizsgálhatunk vele. Szigetelő felületek vizsgálatára fejlesztették ki az atomerő mikroszkópot.
[szerkesztés] Önszerveződő nanoszerkezetek
- A felületek gyakran átrendeződnek jól definiált struktúrájú alakzatokba (surface reconstruction)
- Molekulákból önszerveződő rétegeket képezhetünk. Pl. arany felületre a tiol csoport (SH) szeret kötődni, így egyik végükön tiol csoporttal rendelkező molekulák egy arany felületen önszerveződő monoréteget (self-assambled monolayer, SAM) alkothatnak
- Grafén nanoszalagok létrehozása oxidációval. SiO2 hordozón elhelyezett grafén réteget először oxigén légkörben oxidálunk (~500 OC), aminek hatására kör alakú lyukak jönnek létre. Ezeket 700 OC-os argon atmoszférában hőkezeljük, miközben jól definiált irányú hatszögek jönnek létre. (Reakció: SiO2+C -> SiO + CO) Forrás: Magda Gábor, Dr. Bíró László Péter (MFA)
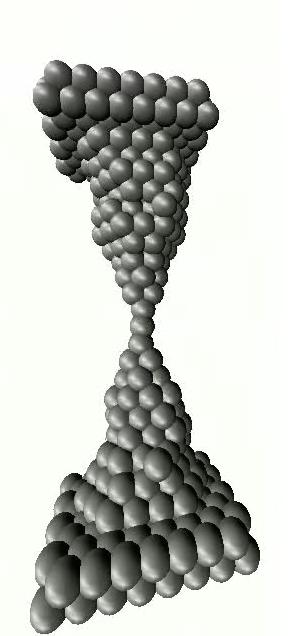
- Bizonyos anyagok szakítás során szeretnek atomi láncokat képezni
Néhány atomból álló kontaktusok vizsgálata:
| 22/a. ábra. Atomi láncképződés. |
| 22/a. ábra. Atomi láncképződés. |
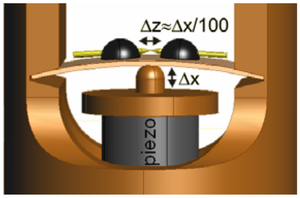
Az atomi kontaktusok vizsgálatára alkalmas mérőberendezések egyike az úgynevezett MCBJ technika (Mechanically Controllable Break Junction technique), melynek felépítése a 3/a. ábrán látható. Egy középen elvékonyított fémszálat két ragasztópötty rögzít egy rugalmas lapkára, amit egy piezo mozgatóval meghajlítunk, így a vezeték két rögzített pontja távolodik egymástól. Már magát a piezo mozgatását is nm alatti pontossággal végezhetjük, a berendezés geometriájából eredő mechanikai áttételnek köszönhetően a szétszakítandó vezeték végeinek elmozdulása a piezo mozgásánál körülbelül két nagyságrenddel kisebb. Így a közvetlenül a szakadás előtt kialakuló atomi kontaktusok vizsgálatára kiemelkedő mechnaikai stabilitás mellett nyílik lehetőség. Miután a minta teljesen elszakadt, újra közelíteni kezdjük a vezetékek végeit, a kontaktus újra felépül. Így egy mintával akár több ezer szakítási görbe is felvehető.
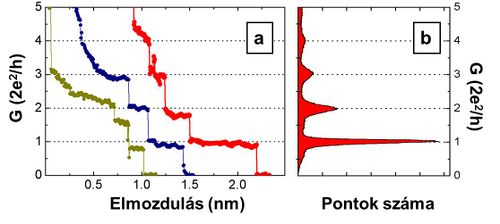
| 20/a. ábra. MCBJ elrendezés vázlata, forrás: Halbritter András PhD dolgozat, 2003. | 20/b. ábra. Arany vezeték szakítása közben mért vezetőképesség görbék. |
A szakítás közben, amikor a vezeték legkisebb keresztmetszetében már csak néhány atom található, a kontaktus vezetőképessége lépcsőzetesen változik (3/b. ábra). Ez a viselkedés elsősorban az anyag atomi felépítésével magyarázható, de az elektronok kvantummechanikai viselkedése is fontos szerepet játszik [hivatkozás a nanovezetékek fejezetre]. A széthúzás közben egy adott atomi konfigurációt először rugalmasan deformálunk, ilyenkor a vezetőképesség nem változik jelentősen. A vezetéket tovább nyújtva egy hirtelen
atomi átrendeződést figyelhetünk meg, ami a vezetőképesség ugrásszerű változását eredményezi. A teljes szétszakadás előtti utolsó plató a legtöbb esetben egy olyan kontaktushoz tartozik, melyben a két elektródát egyetlen atom köti össze. Bizonyos anyagok esetén (például: Au, Cu, Ag) az utolsó platóhoz tartozó vezetőképesség jól reprodukálóan az úgynevezett vezetőképesség kvantummal - egy univerzális állandóval - egyezik meg: 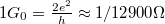 -nak megfelelő értéket vesz fel.
-nak megfelelő értéket vesz fel.
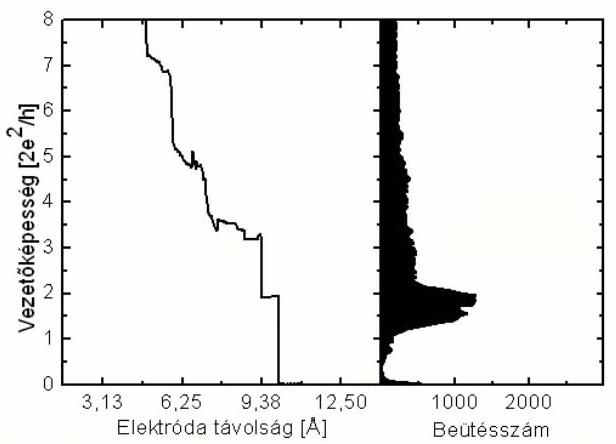
A szakításkor bekövetkező atomi átrendeződések véletlenszerűek, ezért a mért vezetőképesség görbék különbözőek lehetnek, ennek ellenére megfigyelhetőek bizonyos hasonlóságok. Az egyes konfigurációkhoz tartozó platók mindig közel azonos vezetőképességnél találhatóak, azonban ez csak sok - akár több ezer - görbe összehasonlításakor lesz látható. Erre a célra az egyik alapvető kiértékelési mód a mért vezetőképesség görbék hisztogramjának számítása: a hisztogramban csúcsok jelennek azoknál a vezetőképesség értékeknél, ahol a mért vezetőképesség görbékben platók figyelhetőek meg. A hisztogram csúcsai mindig ugyanazokon – a minta anyagára jellemző – vezetőképesség értéknél jelennek meg.
| 21/a. ábra. Vezetőképesség hisztogram készítése az egyedi mért vezetőképesség görbékből. | 21/b. ábra. A kontaktusba molekula épül be - a hisztogramban új csúcs jelenik meg. |
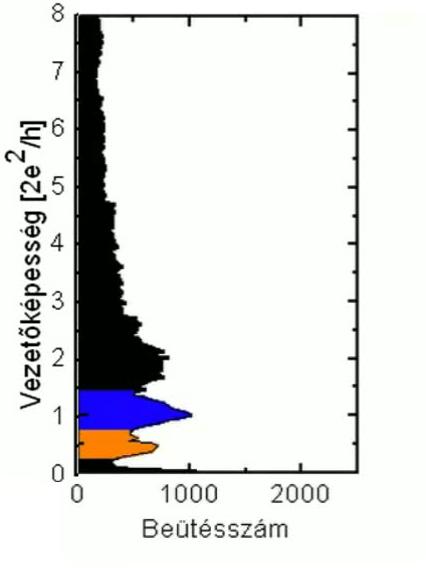
Az MCBJ mérés felhasználható arra is, hogy egyedi molekulák vezetőképességét vizsgáljuk. Ehhez a vezeték folyamatos széthúzása majd összenyomása közben molekulákat juttatunk a kontaktushoz, melyek képesek beépülni a két elektróda közé. A beépült molekula következtében megváltozik a kontaktus vezetőképessége, a mért görbék hisztogramjában egy új csúcs jelenik meg (21/b. ábra). A csúcs helye a beépült molekula vezetőképességét jellemzi.
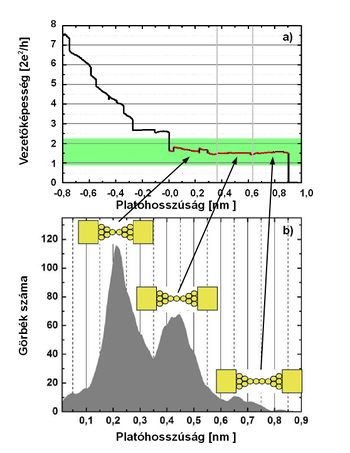
Bizonyos anyagokkal, speciális körülmények között mérve (például arany minta alacsony hőmérsékleten) érdekes jelenség figyelhető meg: az egyedi görbéken megfigyelhető, hogy széthúzáskor az utolsó plató sokszor lényegesen hosszabb a többi platónál. Ez azzal magyarázható, hogy az egyatomos kontaktust széthúzva az nem feltétlenül szakad el egyből, helyette egy több atomból álló atomlánc „húzódik” a két elektróda között. Az atomi láncképződést az utoló plató hosszának statisztikai vizsgálatával lehet kimutatni, a lánc hosszúsága a vezetőképességben mért plató hosszúságával jellemezhető.
| 22/a. ábra. Atomi láncképződés. | 22/b. ábra. Platóhosszúság hisztogram. |
Ha felrajzoljuk, hogy különböző platóhosszúságok milyen gyakorisággal fordulnak elő, akkor az így készített plató hosszúság hisztogramban csúcsok jelennek meg egyenlő távolságokra egymástól. A különböző csúcsok különböző számú atomból álló láncnak felelnek meg, a csúcsok közötti távolság – megfelelő kalibráció után – két szomszédos atom távolságát adja meg a láncban.